Así se calcula la mediana en Excel
Con la función de mediana en Excel puedes averiguar el número situado en la posición central (mediana) dentro de un grupo de cifras. En contraposición a la media, la mediana no proporciona un valor medio, sino la tendencia central dentro de una sucesión de cifras ordenada de menor a mayor.
¿Qué es la mediana?
La mediana es un valor umbral especial que en estadística se denomina cuantil y que divide en dos una determinada sucesión de cifras. Las cifras o valores se disponen en orden ascendente. La mediana determinada muestra el valor numérico que se encuentra en la posición central dentro de la sucesión de cifras analizada.
Función de mediana en Excel: explicación de la sintaxis
En forma de función de Excel, la mediana resulta especialmente práctica para obtener valores centrales concretos. Para determinar la mediana en Excel, desde las versiones de Office 2016 y en Microsoft 365, utiliza la siguiente sintaxis:
La sintaxis de la fórmula de la función de la mediana en Excel está compuesta por la variable numérica “número1” —obligatoria— y las siguientes variables —opcionales— que indican a partir de qué filas de números se debe calcular la mediana. En el caso de las variables “número1”, “número2”, etc. se puede tratar tanto de cifras como también de referencias de celdas.
Cómo utilizar la función de mediana
Si quieres insertar la mediana de un grupo de números en Excel, haz doble clic en una celda y, por ejemplo, introduce =MEDIANA(A1:E1). De esta forma obtendrás el número central de los valores numéricos entre las celdas A1 y E1. De manera alternativa, dentro de una tabla resumen puedes integrar la fórmula de la mediana directamente como una columna o en una fila.
Ejemplo:
- Si buscas la mediana dentro de un grupo impar de valores entre las celdas A3 y A7, introduce
=MEDIANA(A3:A7). De esta forma, obtendrás la mediana 3. - Si buscas la mediana dentro de un grupo par de valores entre las celdas A3 y A8, introduce
=MEDIANA(A3:A8). En este caso, obtendrás la mediana 3,5, es decir, el valor entre las cifras que se encuentren en tercer y cuarto lugar.
¿Qué hay que tener en cuenta en las medianas de Excel?
La función de mediana en Excel es capaz de calcular el valor medio entre 1 y 255 (ancho máximo de columna en Excel). Por lo tanto, ten en cuenta que se debe tratar de valores numéricos, es decir, variables de una escala ordinal. La función ignora texto, nombres, matrices, relaciones y valores lógicos que no contengan números. Por el contrario, la función puede calcular la mediana de valores lógicos y cifras obtenidas mediante fórmulas.
Diferencia entre el valor medio y el valor modal
La mediana indica la tendencia central de los valores numéricos ascendentes en su distribución estadística. Para determinar la tendencia central, en total se pueden utilizar tres posibles valores:
- Mediana: en un grupo ordenado de manera jerárquica, indica el valor situado en la posición central (número central).
- Valor medio: indica la media aritmética que se obtiene al dividir la suma de las cifras proporcionadas por la cantidad de dichas cifras.
- Valor modal: muestra la cifra que más se repite dentro de un grupo numérico.
Si los valores de la lista están distribuidos de manera regular, la mediana se asemejará al valor medio o al valor modal. En caso de que los valores no estén distribuidos de manera uniforme, la mediana suele desviarse del valor medio y del modal.
Número par e impar de valores
Respecto a la cantidad de cifras que se van a tratar, hay que diferenciar entre una cantidad par o impar de cifras:
- Si la cantidad de valores de una lista es impar, la mediana indica la cifra que se encuentra en la posición central del grupo.
- Si la cantidad de valores de una lista es par, la mediana se forma a partir del valor medio (media aritmética) de las dos cifras situadas en el centro del grupo de cifras (denominadas mediana superior e inferior).
Calcular mediana en Excel
La mediana se puede aplicar cuando el valor central de los datos se calcula mediante una escala ordinal, de intervalo o de relación. Las áreas de aplicación más habituales son:
- En la estadística descriptiva, para determinar el valor central en muestras aleatorias
- Para determinar la posición central en distribuciones de probabilidad y variables aleatorias en la teoría de la probabilidad
- Como unidad de medida de métodos de estimación sólidos en distribuciones de valores desconocidas en estadística matemática
Dos ejemplos prácticos de la función de mediana en Excel
Para comprender la utilidad práctica de la función de mediana, vamos a analizar los siguientes ejemplos de aplicación práctica:
Ejemplo 1: mediana para determinar ingresos
Se quiere determinar el valor central de los ingresos anuales de un grupo de siete personas. En función de la distribución del volumen de ingresos, el valor medio puede determinar la renta media, pero puede no dar una imagen realista si el 80 % tiene unos ingresos por debajo de un determinado umbral y el 20 %, por encima. Aquí entra en juego el valor medio.
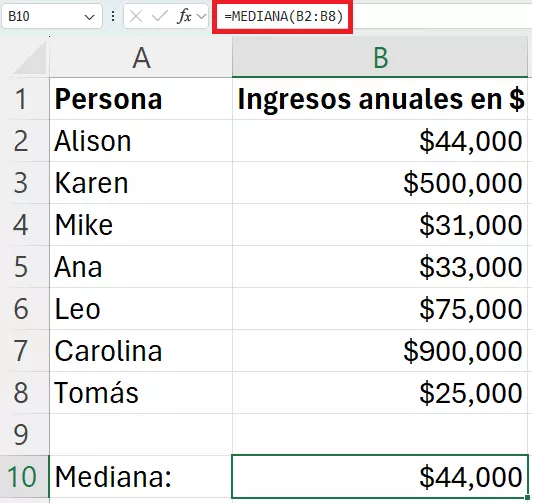
La mediana indica de manera concreta el valor central dentro de la relación de ingresos, es decir, la renta anual de un empleado “normal”. El valor medio, por el contrario, indicaría en este caso unos ingresos anuales medios de $229,714, algo que se puede entender como un nivel de ingresos distorsionado.
En el caso de un grupo de ocho personas, la mediana se determina correspondientemente a través de la media de la mediana inferior y superior (aquí: B2 y B9):
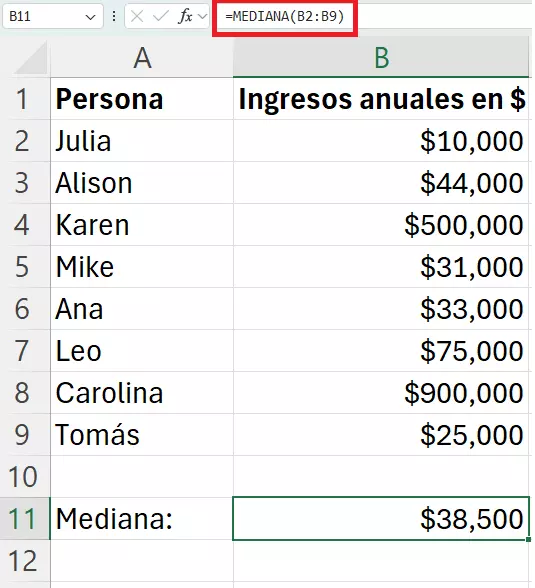
Ejemplo 2: mediana de un rango de notas
Para determinar la tendencia central de un rango de notas, la mediana ayuda a calcular el valor medio dentro de un conjunto de notas. Para calcular la mediana, hemos cambiado las letras de las calificaciones por números: 1 corresponde a una A, 2 a una B, 3 a una C, 4 a una D y 5 a una F.
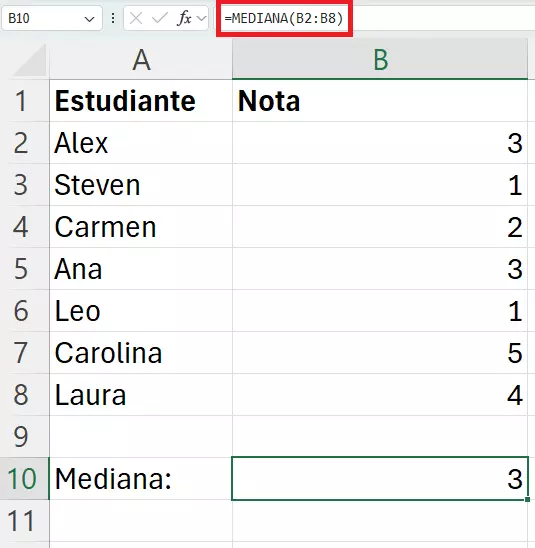
Incluso sin la práctica ayuda de Excel es posible calcular la mediana. Para ello, solo hay que ordenar las cifras de un grupo de menor a mayor y determinar entonces la cifra central (en el caso de un número impar de cifras) o la media de las dos cifras centrales (en el caso de un número par de cifras).

